ゲーム理論を徹底解説:ポーカーのGTOとの関係性

本記事では、GTO(Game Theory Optimal)戦略を理解するために必要なゲーム理論の基本概念について解説し、その理論的背景や計算ロジックについて解説します。
ゲーム理論:基本概念の理解

ゲーム理論とは?

ゲーム理論とは、プレイヤー同士が競争や協力を行う状況を数学的にモデル化し、最適な行動を探求するための学問です。 社会の様々な場面で、人々の意思決定が互いに影響を与え合うため、この理論はビジネスや政治などの分野で広く用いられており、ボードゲームにも適用することができます。
ゲーム理論の分類

実際にゲーム理論を用いて研究するためには、その研究対象がどういったゲームであるのかモデル化して分類する必要があります。 この「分類」を行うために必要な要素(分類方法)は複数ありますが、特にポーカーを理解するために必要な要素を紹介します。
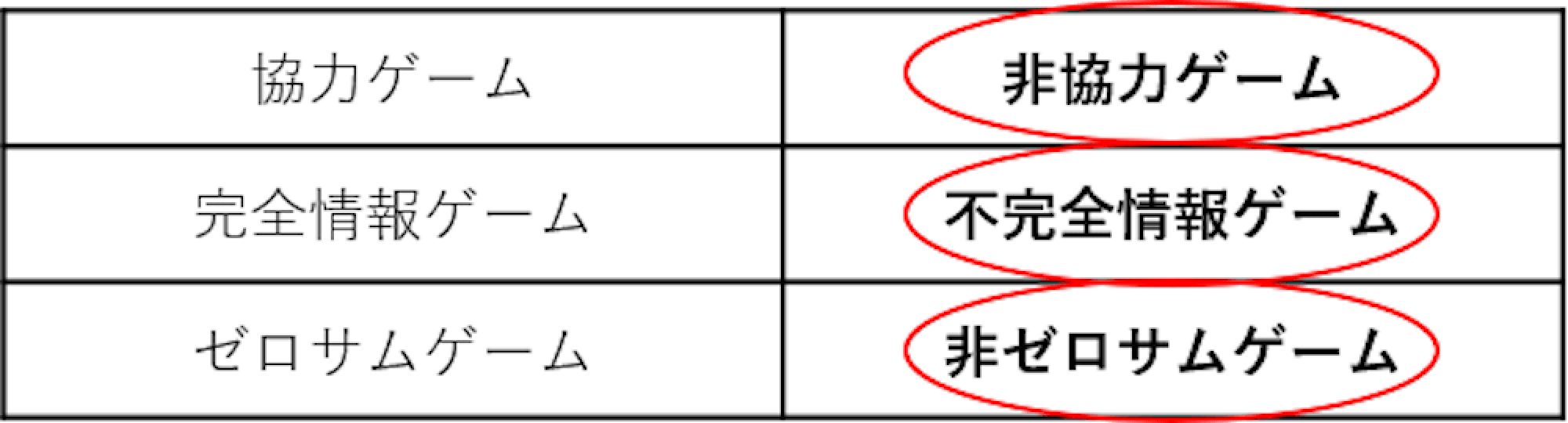
協力ゲームと非協力ゲーム
プレイヤー間がコミュニケーションを取ったり、契約や交渉を行えるか否かによる分類です。
- 協力ゲーム
プレイヤーが互いに協力して利得の最大化を目指す
- 非協力ゲーム
プレイヤーは個々の利益の最大化を目指す
例えば拮抗しているライバル企業との間で、カルテルを結んでお互いに価格競争を止めた場合は協力ゲームであるのに対し、互いに情報が無いなかで行う価格競争などは非協力ゲームとなります。
完全情報ゲームと不完全情報ゲーム
各プレイヤーが、それ以前に行われたすべてのプレイヤーによる意志決定の内容を観察できるか否かで分類します。
- 完全情報ゲーム
プレイヤーによる意思決定の内容を観察できるゲーム
- 不完全情報ゲーム
プレイヤーによる意思決定の内容を観察できないゲーム
将棋やチェスは完全情報ゲームであるのに対し、麻雀やポーカーは相手の手が見えないため不完全情報ゲームとなります。
ゼロサムゲームと非ゼロサムゲーム
各プレイヤーの利得の総和がゼロになるかどうかによる分類です。
- ゼロサムゲーム
誰かが利益を上げれば、他の誰かの損失となるゲーム
- 非ゼロサムゲーム
参加者の利益と損失の総和が0にならないゲーム
例えば外国為替取引(FX)の場合、一方の為替レートが上がれば、もう一方のレートは必ず下がることになるため、ゼロサムゲームとなります。株式投資は市場の参加者全員が利得を獲得できることもあるため非ゼロサムゲームとなります。
以上の観点から自分が直面している対象の特徴を捉え、分類する必要があります。
ゲーム理論上の最適解

ゲーム理論上の最適解を考えるためには、研究対象を適切にモデル化し分類する必要があります。
本記事においては、ゲーム理論における様々なモデルを解説するのではなく、「ポーカー」というゲームの最適解を導く上で、根幹となる概念について解説します。
ナッシュ均衡
恐らく本記事を読んでいる人は聞いたことがあるかもしれませんが、ゲーム理論上の最適な戦略を考えるうえで「ナッシュ均衡」の理解は必要不可欠となります。
ナッシュ均衡とは、全てのプレイヤーが自分の戦略を変えることで利得を拡大することができない状態を指します。
二人でのじゃんけんを例に取って考えてみましょう。
AとBの二人はじゃんけんを何度も繰り返すとします。Aは「最初はグー」の掛け声につられていつもグーばかり出すということにBが気づいたとします。
そうするとBは意識的にパーを多く出すようになります。Bがパーばかり出すということに気づいたAは意識的にチョキを多く出します。これに気づいたBはグーを多く出すようになります。
このように、相手の傾向を把握して自分の出す手の頻度を�少しずつ調節する、ということを繰り返していくと、どのようになるでしょうか。最終的には互いにグーチョキパーを33.3%ずつ出すようになります。
この均衡の取れた状態がナッシュ均衡です。
この状態から、Aがパーを33.3%以上の頻度で出すようになったらどうなるでしょうか?
Bは33.3%の頻度で出しているのでお互いの勝率は実は変わりません。しかし、パーばかりだしているということがBに分かってしまうとBはチョキの頻度を少し多くすることで勝率を上げることができてしまいます。
つまり、この状態はナッシュ均衡ではないといえます。
このように互いの戦略を変えることで利得を拡大することができない状態を「ナッシュ均衡」と呼びます。
混合戦略と純粋戦略
ゲーム理論上最適とされる戦略が常に一つの決められた戦略(純粋戦略)であるか、複数の戦略を確率的に選択する戦略(混合戦略)であるのかを決定する概念です。
これはゲームの特性に依存しますが、常に一つの戦略が他の戦略よりも利益的である場合には純粋戦略が適用される(支配戦略)のに対し、支配戦略がない場合は混合戦略が採用されます。
混合戦略を用いる場合、自分が取るべき戦略を確率的に選択する必要があります。この戦略の確率分布を算出することが、最適な混合戦略を導き出す鍵となります。
パレート最適
パレート最適とはゲーム理論上「誰かの状況を改善しようとすれば、他の誰かの状況を悪化させてしまう状態」です。
この概念は元々資源の効率的な使用のために提唱されました。 つまり、「最も無駄がなく効率的に資源を消費できている状態」と言えます。
一般的に協力ゲームで用いられることが多く、各プレイヤーが個々の利得の最大化を目的としている場合ゲーム理論上最適な戦略はパレート最適とならないことが多くあります。
パレート最適はポーカーで使われることはそこまで多くありませんが、 例えばトーナメントにおいてあと一人が飛んだ場合に入賞が確定するような状況において、あえてテーブルの多くの人間がショートのオールインにコールする、といった事例が考えられます。この時、テーブルにいる人が入賞するという共通の目的のために、協力してショートを飛ばすことがパレート最適の考え方から肯定されます。
具体例

以下にゲーム理論における代表的な例題を示し、上述した概念から解説していきます。
囚人のジレンマ
二人の囚人AとBがいます。警察は彼らが一緒に罪を犯したことを疑っていますが、証拠が不十分なため、囚人に告発させようとしています。
囚人たちには、
- 黙秘
- 他の囚人を告発
の二つの選択肢が与えられています。 そして、この選択には次のような結果が生じます。

二人の囚人はお互いにコミュニケーションを取れず、自分個人の刑期しか考えていないと仮定すると、以下のように分類することができます。
ここで、自分自身の利益を最大化するためには、どうすればいいか考えます。
囚人A目線で、場合分けをして考えてみましょう。
- 囚人Bが黙秘:
- 囚人Aが黙秘:Aは懲役2年
- 囚人Aが告発:Aは懲役0年
- 囚人Bが告発:
- 囚人Aが黙秘:Aは懲役10年
- 囚人Aが告発:Aは懲役5年
以上より、囚人Bがどのような選択をしても、囚人Aは告発することで懲役を減らすことができます。 これはお互いの囚人に対して言えることであるため、互いに合理的な判断をした場合二人とも告発し、両方とも懲役5年となります。
つまり、個々の合理的な判断は、集団として必ずしも最適な結果にはなりえないということを表しています。 この状態がナッシュ均衡の状態となります。
一方で、互いの囚人が密かにコミュニケーションを取ることができたと仮定すると、二人で結託し、お互いに黙秘を選ぶことができます。 その場合両方とも懲役2年となり、この状態が囚人全体の利益が最大化されたパレート最適な状態であるといえます。
巡回セールスマン問題(TSP)
セールスマンが複数の都市を訪れ、その後出発点に戻る予定です。それぞれの都市をちょうど1回だけ訪れ、かつ全体の旅行距離を最小にしたいと考えています。彼はどの都市からどの都市へ移動すればよいでしょうか?
この問題は、一見すると単純に見えますが、実は非常に複雑です。 というのも、都市の数が増えると、全ての可��能な経路の組み合わせが指数関数的に増加するためです。このため、大規模なTSPは、最適な経路を見つけるのが難しくなります。
例えば3都市であれば、最初に訪れ得る都市は3通りあり、次に訪れる都市は2通りであり合計3×2の6通りから最短な経路を探せばいいことになります。
一方で10都市となると、最初に訪れる都市は10通りあり、次に訪れる都市は9通り、その次は8通り…と合計で10!=3,628,800通りあり、この中から最適な経路を考えることは非常に困難になります。
このように、可能な解の数が非常に大きい問題を「組み合わせ爆発」といいます。このため、大規模なTSPを解くためには、ヒューリスティクス(近似的な手法)や他の効率的なアルゴリズムが使われます。
例えば上記の問題であれば、セールスマンが次に行く都市は必ず隣接した都市であるという制約を加えることで、組み合わせの数が大幅に減少し、計算量を削減することができます。
ポーカーのGTO解析では、類似のアプローチが取られます。
ポーカーでは以下の要素を考慮する必要があります
- ポジション
- ハンド
- ボード
- アクション
- ベットサイズ
- ターンカード
- リバーカード
これらの要因を考慮して期待値(EV)が最も高くなるアクションを決定するがあります。
しかし、これらの要因が多岐にわたるため、計算量が非常に大きくなる可能性があります。 そのため、一般的にはベットサイズを1BB(ビッグブラインド)毎に連続的に変化させるのではなく、特定の数値に限定したり、ハンドレンジを限定することで計算を簡略化します。
ゲーム理論とポーカー

ポーカーも先述したゲームと同様にゲーム理論的な観点から分析をすることが可能です。
ポーカーの分類
ポーカーは先ほどの要素から考えると以下のように分類することができます。
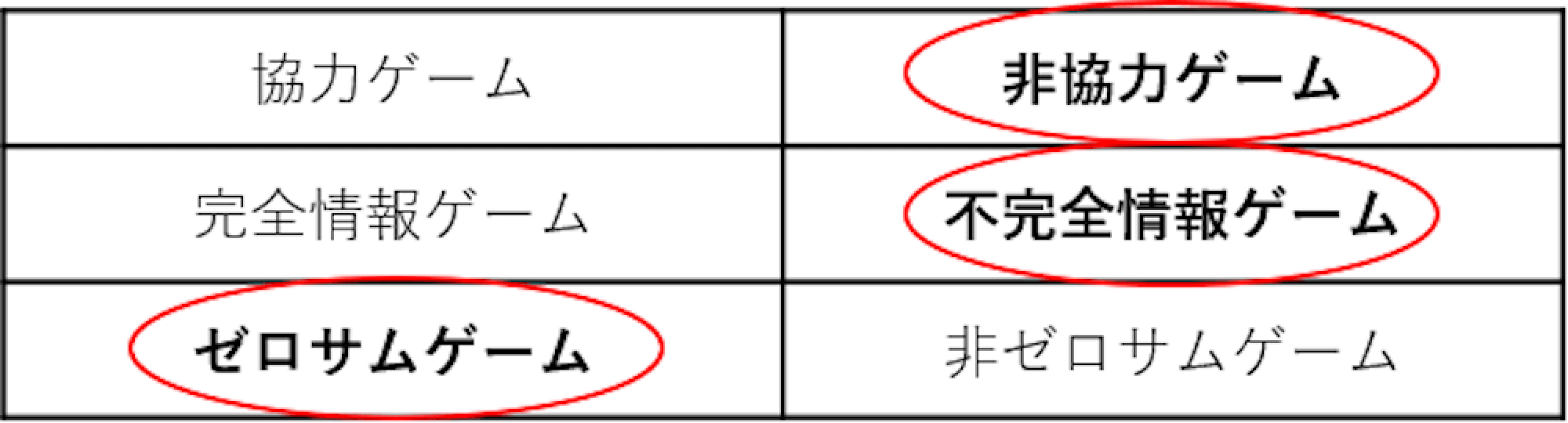
ポーカーのナッシュ均衡解

ポーカーにおいてもナッシュ均衡解は存在します。
お互いのプレイヤーが戦略を変えることで利益をこれ以上増やすことができない戦略が存在し、それがGTO戦略と呼ばれています。
つまり、ゲーム数を∞回行うと仮定した場合に、GTO戦略に対して勝ち越すことのできる戦略は存在せず、互いにGTO戦略同士で戦った場合に、お互いの利得は0になります。
ポーカーにおける戦略
では、ポーカーにおけるナッシュ均衡解、つまりGTO戦略とはどのような戦略になるのでしょうか?
ポーカーはナッシュ均衡を基に計算されたアクションの確率分布が存在し、その確率分布に基づいてプレイする必要があります。
どれか一つのアクションの確率が100%の場合、そのハンドは純粋戦略を取るべきであり、複数のアクションに確率が存在する場合は混合戦略となります。
- 混合戦略が採用される場合
確率が存在しているアクションはどれを選んでも期待値は変わりません。そのため、頻度が低いアクションを選択しても期待値は損失しません。
- 純粋戦略が採用される場合
それ以外のアクションを選択すると期待値を必ず損失します。これは混合戦略でも同じであり、頻度が0%のアクションを選択すると期待値を必ず損失します。
ポーカーがゼロサムゲームであるという特徴を考えると、こちらに損失が発生しているということは相手に利得が生じているということになります。
では、このアクションの確率分布をどのように計算しているのか次節にて解説します。
計算ロジック
ポーカーにおけるゲーム理論的に最適とされるアクションの決定は確率分布に基づくと解説しました。 では、その確率分布はどのように計算されるのでしょうか?
ポーカーも他のゲームと同様にモデル化してとらえる必要があります。
ポーカーでは様々な要素があり、それらをモデル化した上で、戦略のExpected Value(EV)を比較することでナッシュ均衡解を計算することができます。
計算のアルゴリズムは一般的にCFR(Counterfactual Regret Minimization)アルゴリズムが採用されており、以下のような手順になっています。
- 完全にランダムな戦略を使用して、AとBの2人のプレイヤーで開始します。
- 次に、プレイヤーAの戦略から、EVを下げているアクションの確率分布を修正し、Aが新しい戦略を取った場合のプレイヤーBのEVの計算をします。
- 次に、プレイヤーBの戦略から、EVを下げているアクションの確率分布を修正し、Bが新しい戦略を取った場合のプレイヤーAのEVの計算をします。
- 同様に、プレイヤーAの新しい戦略をさらに修正し、プレイヤーBにそれを活用させます。
- これを均衡(とみなせる)となるまで繰り返し行います。
2人のじゃんけんを例にとって考えてみましょう。
- まずはランダムに、Aはグーチョキパーを(70%,20%,10%)で出すとし、Bはグーチョキパーを(10%,20%,70%)で出すとします。
- まずAはグーを70%で出すことの損失、チョキを20%で出すことの損失、パーを10%で出すことの損失を計算します。その結果、グーを出している時に大きく損失が発生していることがわかったので、グーの頻度を40%にまで下げ、チョキとパーの頻度をそれぞれ20%、10%上げ、(40%,40%,20%)とすると、期待値の損失が抑えられていることがわかりました。
- このAの確率分布を使って、Bの確率分布を修正することを考えます。Bは現在(10%,20%,70%)で出しており、パーとチョキの頻度を下げると期待値がプラスになることが分かったので確率分布を(40%,10%,50%)としました。
- これに対してAの方でも同様に確率分布の修正を行います。
- この操作を繰り返し行い、互いに(33%,33%,33%)となります。この状態は、これ以上期待値を上げる戦略がなくなった均衡地点(ナッシュ均衡)となります。
ここでのスタート地点の決め方(上記ではランダムとした)や確率分布の修正はモデルによって異なり、各GTOツールが精度の向上を目指している領域になります。
エクスプロイト戦略

本節ではGTO戦略から少し離れ、より実践的なエクスプロイト戦略について解説します。
エクスプロイト戦略とは「相手の弱点を突く」戦略であり、あえて自分がGTO戦略から外れたプレイを行い、より利得の拡大を狙う戦略になります。 エクスプロイト戦略はGTO戦略をしっかりと理解していなければ、適切に行うことが難しくなります。
例えばブラフが多いプレイヤーに対してコールやレイズを多くすることは利益的ではありますが、そもそも基準となる頻度やアクションが分からなければ、相手が本当にブラフが多いのかどうかも分かりません。つまり、自分の感覚に依存したあやふやな戦略となってしまいます。
ゲーム理論においては「最適反応戦略」という概念が存在します。これは他のプレイヤーの戦略に対して自身の利益を最大化する戦略ということを示します。 もちろんお互いにナッシュ均衡解同士で戦っている場合には最適反応戦略自体がナッシュ均衡解となります。
しかし、ポーカーにおけるナッシュ均衡解は非常に複雑な確率分布であり、それを完全に再現することは�人間には到底不可能です。 言い換えると、どのようなトッププロにも必ず癖があるため、そのプレイヤーの癖に対して自分の利益を最大化できるように組み立てた戦略が最適反応戦略(エクスプロイト戦略)になります。
ただ、エクスプロイト戦略を取るということはあえてGTO戦略から外れた戦略を取るため、相手にエクスプロイトされるリスクがあります。
ポーカーは長期的にプレーして利益を最大化することが重要な競技であるという特質を考えると、まずはGTO戦略への理解を深めることが上達の近道であることは自明です。
GTO戦略をしっかりと学ぶことができれば、エクスプロイト戦略はある程度理解できるようになるため、まずはしっかりとGTO戦略についての理解を深めていきましょう。
まとめ

本記事ではゲーム理論について解説すると共に、ゲーム理論がポーカーにどのように関わっているのかについて解説しました。 ポーカーはゲーム理論上解析可能なゲームであり、ゲーム理論を理解することはポーカーの上達に大きく寄与します。
しかし本当にポーカーを強くなりたいという場合は理論の勉強だけでは不十分であり、ゲーム理論から導き出されたGTO戦略を学習しなければなりません。
GTO戦略は複雑な確率分布によって構成されているため、ポーカーのGTO解析ツールを使い、途方もない数の多くのハンド数を解析し、地道に学習していくしか方法はありません。
ゲーム理論からポーカーを解析すると、そのゲームの複雑性がより露呈され、上達への近道など存在しないということが分かっていただけたかと思います。 地道な分析と学習からポーカーの実力を向上していきましょう。
