Game Theory Thoroughly Explained: Poker's Relationship to the GTO

In this article, we explain the fundamental concepts of GTO (Game Theory Optimal) strategy, providing an explanation of its theoretical background and computational logic.

Understanding the Basic Concepts of Game Theory

What is Game Theory?

Game Theory is the study that mathematically models situations where players compete or cooperate with each other to explore optimal actions. It is widely used in various fields such as business and politics, as decisions made by people in society often affect each other. This theory can also be applied to board games.

Classifications of Game Theory

To study using game theory, it is necessary to model and classify the type of game being researched. There are several elements (classification methods) necessary for this ’classification’, but I will introduce the elements particularly necessary for understanding poker.

Cooperative and Non-Cooperative Games

Classification based on whether players can communicate with each other, and whether they can make contracts or negotiate.

• Cooperative Games

Games where players cooperate with each other to maximize their gains

• Non-Cooperative Games

Games where players aim to maximize their individual benefits

For example, in a situation where rival companies stop price competition by forming a cartel, it is a cooperative game. In contrast, price competition conducted without shared information among the players is a non-cooperative game.

Perfect Information Games and Imperfect Information Games

Classification based on whether each player can observe the decisions made by all other players in previous plays.

• Perfect Information Games

Games where players can observe the decisions made by others

• Imperfect Information Games

Games where players cannot observe the decisions made by others

Chess and Shogi are perfect information games, whereas Mahjong and Poker, where players cannot see each other’s hands, are imperfect information games.

Zero-Sum Games and Non-Zero-Sum Games

Classification based on whether the total gain of all players equals zero.

• Zero-Sum Games

Games where someone’s gain is another’s loss

• Non-Zero-Sum Games

Games where the total of gains and losses among participants does not necessarily equal zero

For instance, in foreign exchange trading (FX), if one currency’s rate increases, the other necessarily decreases, making it a zero-sum game. Stock trading can be a non-zero-sum game as all market participants can potentially gain profits.

From the above perspectives, it is necessary to capture the characteristics of the situation you are facing and classify them accordingly.

Optimal Solutions in Game Theory

To consider the optimal solution in game theory, it is essential to properly model and classify the subject of study.

In this article, instead of explaining various models in game theory, we will focus on explaining the core concepts that lead to the optimal solution for the game of ‘Poker’.

Nash Equilibrium

You may have heard of it if you are reading this article, but understanding the “Nash Equilibrium” is essential when considering the optimal strategy in game theory.

Nash Equilibrium refers to a state where none of the players can increase their gains by changing their strategies.

Let’s consider the example of Rock-Paper-Scissors between two people.

Suppose two people, A and B, repeatedly play rock-paper-scissors. Let’s say B notices that A always throws rock because of the initial call “First is rock.”

Then B starts to throw paper more often consciously. Once A notices B is mostly throwing paper, A begins to throw scissors more. Realizing this, B then starts throwing rock more frequently.

If they continue to adjust the frequency of their choices based on the opponent’s tendencies, what happens? Eventually, they both start throwing rock, paper, and scissors each 33.3% of the time.

This balanced state is the Nash Equilibrium.

What happens if A starts throwing paper more than 33.3% of the time from this state?

Since B is throwing each at 33.3% frequency, their winning rates don’t actually change. However, if A’s predominant paper throwing becomes apparent to B, B can increase his winning rate by slightly increasing the frequency of scissors.

Thus, this state is not a Nash Equilibrium.

This is how the state where none of the players can increase their gains by changing their strategies is called a ”Nash Equilibrium”.

Mixed Strategy and Pure Strategy

This concept determines whether the optimal strategy in game theory is always a single defined strategy (Pure Strategy) or a strategy that probabilistically chooses between multiple strategies (Mixed Strategy).

This depends on the characteristics of the game, but when one strategy is always more beneficial than others, a Pure Strategy is applied (dominant strategy). In contrast, when there is no dominant strategy, a Mixed Strategy is adopted.

When using a Mixed Strategy, it is necessary to probabilistically choose the strategy you should take. Calculating the probability distribution of this strategy is key to deriving the optimal mixed strategy.

Pareto Optimality

Pareto Optimality in game theory refers to a situation where “improving someone’s situation would worsen someone else’s.”

This concept was originally proposed for the efficient use of resources. In other words, it can be described as ”the state where resources are consumed most efficiently without waste.”

It is commonly used in Cooperative Games. In cases where each player aims to maximize their individual gains, the optimal strategy in game theory often does not result in Pareto Optimality.

Pareto Optimality is not often used in poker, but for example, in a tournament situation where one more player’s elimination guarantees qualification, it’s conceivable that many players at the table may call a short stack’s all-in. In this case, the cooperation to eliminate the short stack for the common goal of qualifying can be justified from the perspective of Pareto Optimality.

Concrete Examples

Below, we present a classic example in game theory and explain it using the concepts discussed above.

The Prisoner's Dilemma

There are two prisoners, A and B. The police suspect they have committed a crime together, but lack sufficient evidence, so they try to get the prisoners to accuse each other.

The prisoners have two choices:

1. Remain Silent
2. Accuse the Other Prisoner

The consequences of these choices are as follows:

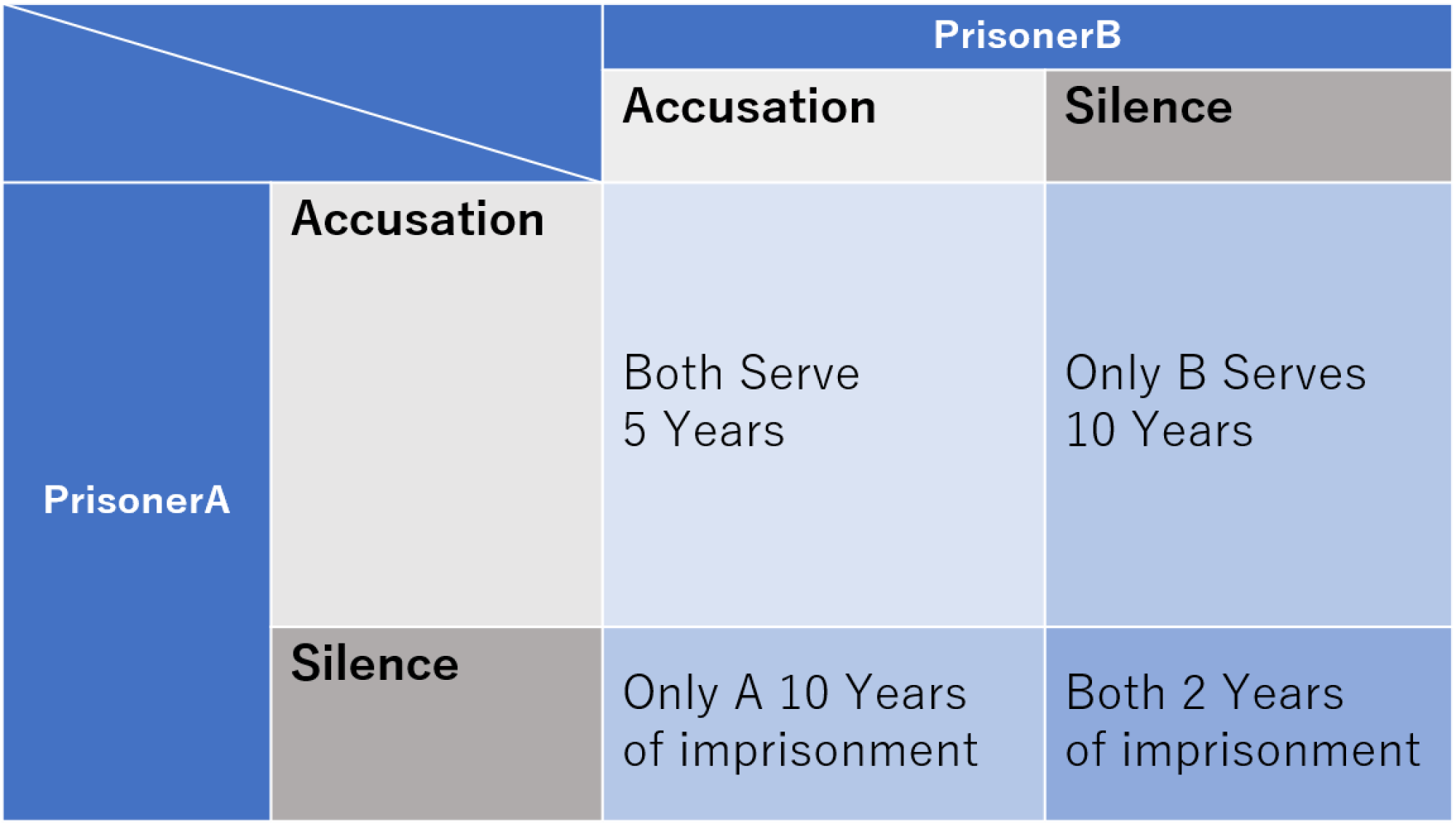
Assuming the two prisoners cannot communicate with each other and are only considering their own sentences, we can classify their situation as follows:
 

Now, let’s think about how to maximize self-interest. Let’s consider the situation from Prisoner A’s perspective.

• If Prisoner B Remains Silent:
  • If Prisoner A remains silent: A serves 2 years
  • If Prisoner A accuses: A serves 0 years

• If Prisoner B Accuses:
  • If Prisoner A remains silent: A serves 10 years
  • If Prisoner A accuses: A serves 5 years

From this, no matter what Prisoner B chooses, Prisoner A can reduce their sentence by accusing. The same applies to Prisoner B. Therefore, if both make rational decisions, they will both accuse each other, resulting in 5 years of imprisonment for both.

This situation demonstrates that individual rational decisions do not always lead to the best outcome for the group. This state is the Nash Equilibrium.

On the other hand, if we assume the prisoners can secretly communicate, they could conspire to both remain silent. In that case, both would serve 2 years, and this situation would be the Pareto Optimal state where the collective benefit of the prisoners is maximized.

Traveling Salesman Problem (TSP)

A salesman plans to visit multiple cities and then return to the starting point. He wants to visit each city exactly once, minimizing the total travel distance. Which cities should he travel to and in what order?

This problem seems simple at first glance, but it is actually very complex. This is because the number of possible route combinations increases exponentially with the number of cities. Hence, finding the optimal route in a large-scale TSP becomes challenging.

For example, with 3 cities, there are 3 ways to choose the first city to visit, 2 ways for the next, making a total of 3×2=6 combinations to find the shortest route.

However, with 10 cities, there are 10 choices for the first city, 9 for the next, 8 for the one after, and so on, totaling 10! = 3,628,800 combinations, making it extremely difficult to determine the best route.

Such problems, where the number of possible solutions is very large, are known as ’combinatorial explosion’. Therefore, to solve large-scale TSPs, heuristics (approximate methods) or other efficient algorithms are used.

For example, in the problem above, by adding a constraint that the salesman must always go to an adjacent city next, the number of combinations significantly decreases, reducing the computational effort.

In poker GTO analysis, a similar approach is taken.

In poker, the following elements need to be considered:

• Position
• Hand
• Board
• Action
• Bet Size
• Turn Card
• River Card

Considering these factors, the action with the highest Expected Value (EV) must be determined.

However, due to the wide range of these factors, the computational effort can become very large. Therefore, instead of continuously varying the bet size by 1BB (Big Blind), it’s common to limit it to specific values or restrict the hand range to simplify calculations.

Game Theory and Poker

Poker can also be analyzed from a game theoretical perspective, similar to the games mentioned earlier.

Classification of Poker

Considering the previously mentioned elements, poker can be classified as follows:

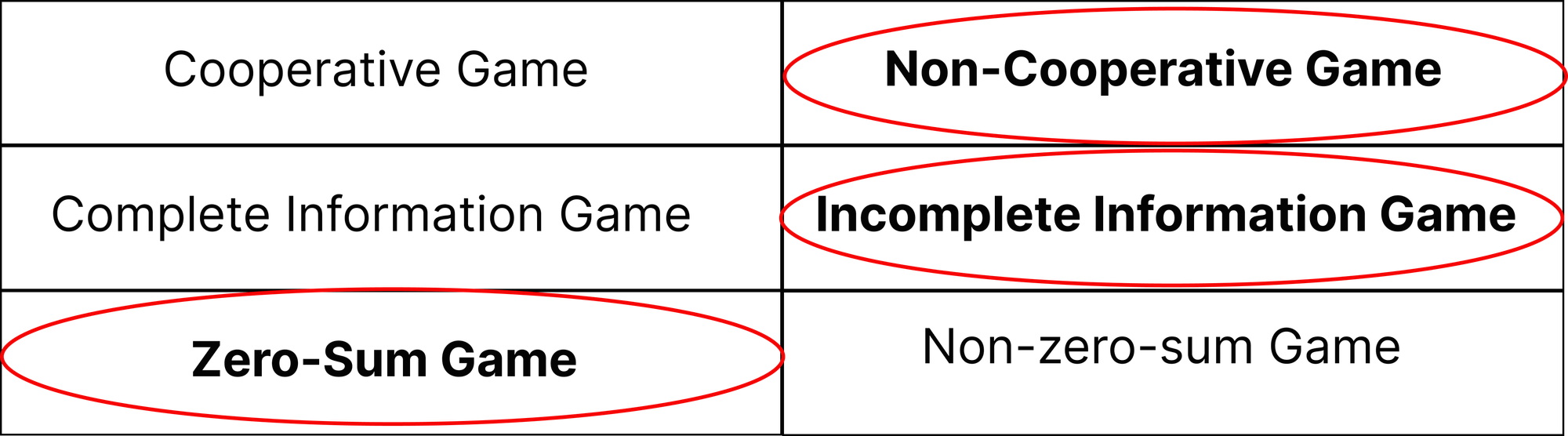
Nash Equilibrium in Poker

In poker, there exists a Nash Equilibrium solution.
A strategy exists where neither player can increase their profit by changing their strategy, and this is known as GTO strategy.

In other words, assuming the game is played ∞ times, there is no strategy that can consistently beat a GTO strategy. When both players use GTO strategies against each other, their gains will average out to zero.

Strategy in Poker

So, what constitutes a Nash Equilibrium solution, or in other words, a GTO strategy in poker?

In poker, there is a probability distribution of actions calculated based on Nash Equilibrium, and it is necessary to play according to this distribution.

If the probability of one action is 100%, that hand should adopt a Pure Strategy. If there are probabilities for multiple actions, it’s a Mixed Strategy.

• When a Mixed Strategy is Adopted

The expected value remains the same regardless of which action with a probability is chosen. Therefore, choosing an action with a lower frequency will not reduce the expected value.

• When a Pure Strategy is Adopted

Choosing any other action will always result in a loss of expected value. This is also true for mixed strategies; choosing an action with a 0% frequency will always lead to a loss in expected value.

Considering that poker is a Zero-Sum Game, a loss on our part means a gain for the opponent.

Next, we will explain how this probability distribution of actions is calculated.

Calculation Logic

We have explained that the determination of theoretically optimal actions in poker is based on a probability distribution. So, how is this probability distribution calculated?

Like other games, poker needs to be modeled. In poker, various elements exist, and these can be modeled to compare the Expected Value (EV) of strategies to calculate the Nash Equilibrium solution.

The algorithm commonly used for calculation is the CFR (Counterfactual Regret Minimization) algorithm, which follows these steps:

1. Start with two players, A and B, using completely random strategies.
2. Then, modify the probability distribution of actions that reduce EV in Player A’s strategy and calculate Player B’s EV if A adopts a new strategy.
3. Next, modify the probability distribution of actions that reduce EV in Player B’s strategy and calculate Player A’s EV if B adopts a new strategy.
4. Similarly, further adjust Player A’s new strategy and let Player B leverage it.
5. Repeat this process until equilibrium (or what is considered equilibrium) is reached.

Let’s think about it in the context of Rock-Paper-Scissors with two players.

1. Initially, let A throw rock-paper-scissors at (70%, 20%, 10%), and B throws at (10%, 20%, 70%).
2. A calculates the loss of throwing rock at 70%, scissors at 20%, and paper at 10%. It’s found that there is a significant loss when throwing rock, so A reduces rock to 40% and increases scissors and paper to 40% and 20%, respectively, finding that expected value loss is reduced.
3. Using A’s probability distribution, B’s distribution is modified. B currently throws at (10%, 20%, 70%), and it’s found that reducing paper and scissors frequency increases the expected value, so the distribution is adjusted to (40%, 10%, 50%).
4. A similarly adjusts their probability distribution in response.
5. This process is repeated until both reach (33%, 33%, 33%). This state is the equilibrium point (Nash Equilibrium), where no strategy can further increase the expected value.

The starting point (random in this case) and adjustments to the probability distribution vary depending on the model, and this area is where various GTO tools aim to improve accuracy.

Exploit Strategies

In this section, we move away from GTO strategies and explain more practical exploit strategies.

Exploit strategies are about ‘exploiting the opponent’s weaknesses’, deliberately deviating from GTO strategies to aim for greater gains. It’s difficult to appropriately implement exploit strategies without a solid understanding of GTO strategies.

For example, calling or raising more against a player who bluffs a lot is profitable, but without knowing the standard frequency or actions, you can’t tell if the opponent is indeed bluffing more than usual. In other words, it becomes a vague strategy dependent on your own perception.

In game theory, there is a concept of ’best response strategy’, which is a strategy that maximizes one’s profit against other players’ strategies. Of course, when both players are battling with Nash Equilibrium strategies, the best response strategy itself becomes a Nash Equilibrium.

However, the Nash Equilibrium in poker is incredibly complex, and it’s virtually impossible for humans to fully replicate it. In other words, since even top pros have their tendencies, the strategy that maximizes your profit against their playstyle becomes the best response strategy (exploit strategy).

But adopting an exploit strategy means deliberately deviating from GTO strategies, which also brings the risk of being exploited by the opponent.

Considering poker’s nature of maximizing profits over the long term, it’s evident that deepening your understanding of GTO strategies is a shortcut to improvement.

If you can thoroughly learn GTO strategies, you will be able to grasp exploit strategies to some extent, so first, focus on deepening your understanding of GTO strategies.

Conclusion

In this article, we explained game theory and how it relates to poker. Poker is a game that can be analyzed using game theory, and understanding game theory significantly contributes to improving in poker.

However, if you truly want to become strong in poker, studying theory alone is insufficient; you must learn the GTO strategies derived from game theory.

Since GTO strategies are composed of complex probability distributions, the only way to learn them is to use poker GTO analysis tools, analyze a vast number of hands, and diligently study.

Analyzing poker through game theory exposes the complexity of the game, and you’ll realize that there are no shortcuts to improvement. Let’s improve our poker skills through meticulous analysis and learning.